GitHub

Glacial cycle

We now want to provide an example that presents:

  • a heterogeneous lithosphere thickness
  • a heterogeneous upper-mantle viscosity
  • a stack of few viscous channels
  • a more elaborate load that evolves over time
  • changes in the sea-level

For this we run a glacial cycle of Antarctica with lithospheric thickness and upper-mantle viscosity from (Wiens et al., 2022) and the ice thickness history from (Peltier et al., 2018). We start by generating a ComputationDomain with intermediate resolution for the sake of the example and load the heterogeneous lithospheric from (Pan et al., 2022) thanks to the convenience of load_dataset:

using CairoMakie, FastIsostasy

N = 140
Omega = ComputationDomain(3500e3, 3500e3, N, N)     # 100 km resolution
(; Lon, Lat) = Omega
c = PhysicalConstants()

(_, _), Tpan, Titp = load_lithothickness_pan2022()
Tlitho = Titp.(Lon, Lat) .* 1e3                     # convert from m to km

function niceheatmap(X)
    fig = Figure(size = (800, 700))
    ax = Axis(fig[1, 1], aspect = DataAspect())
    hidedecorations!(ax)
    hm = heatmap!(ax, X)
    Colorbar(fig[1, 2], hm, height = Relative(0.6))
    return fig
end
niceheatmap(Tlitho)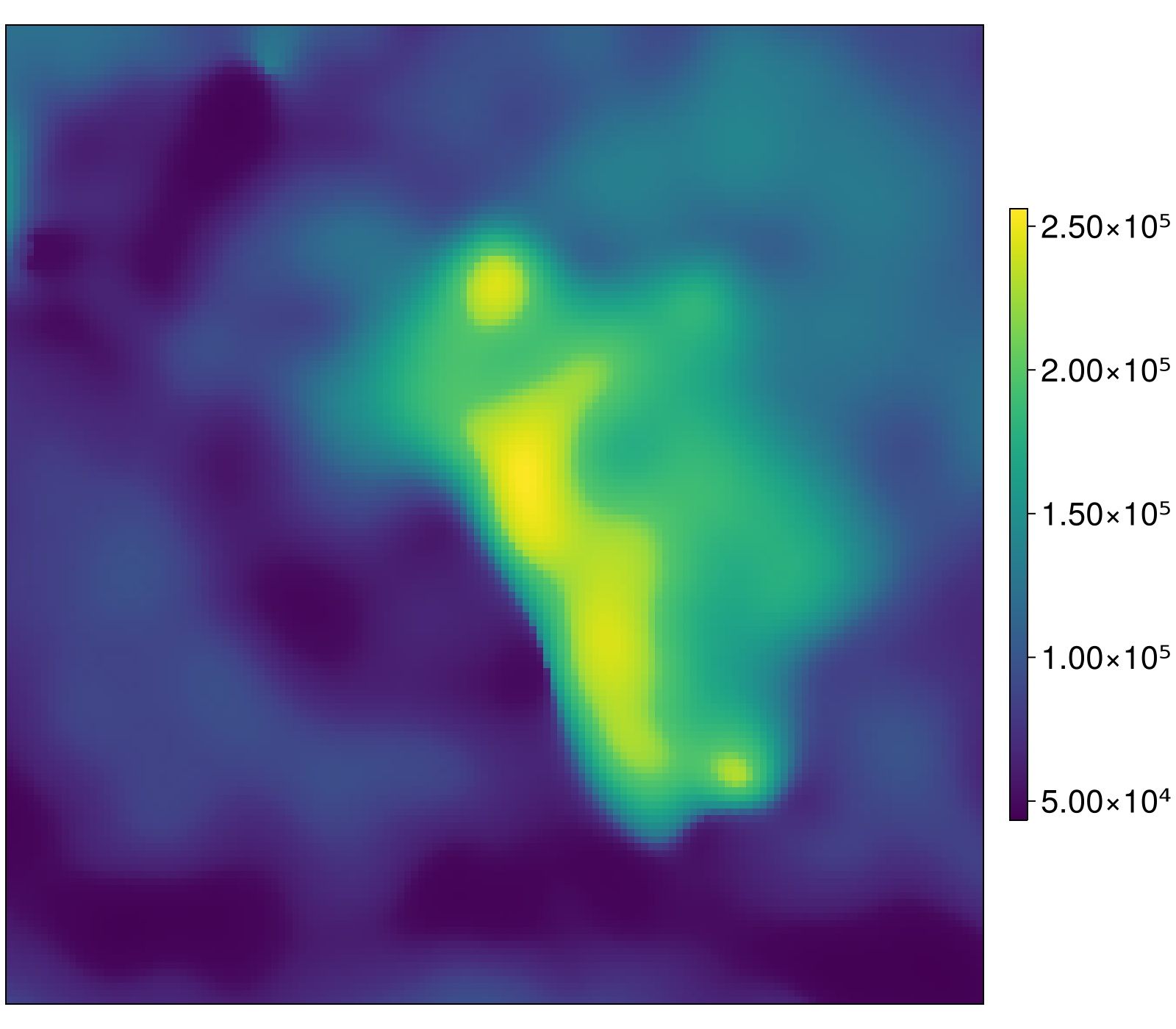
Example block output

In a similar way, we can load the log-viscosity field from (Pan et al., 2022) and plot it at about 300 km depth

(_, _, _), _, logeta_itp = load_logvisc_pan2022()
logeta300 = logeta_itp.(Lon, Lat, c.r_equator - 300e3)
niceheatmap(logeta300)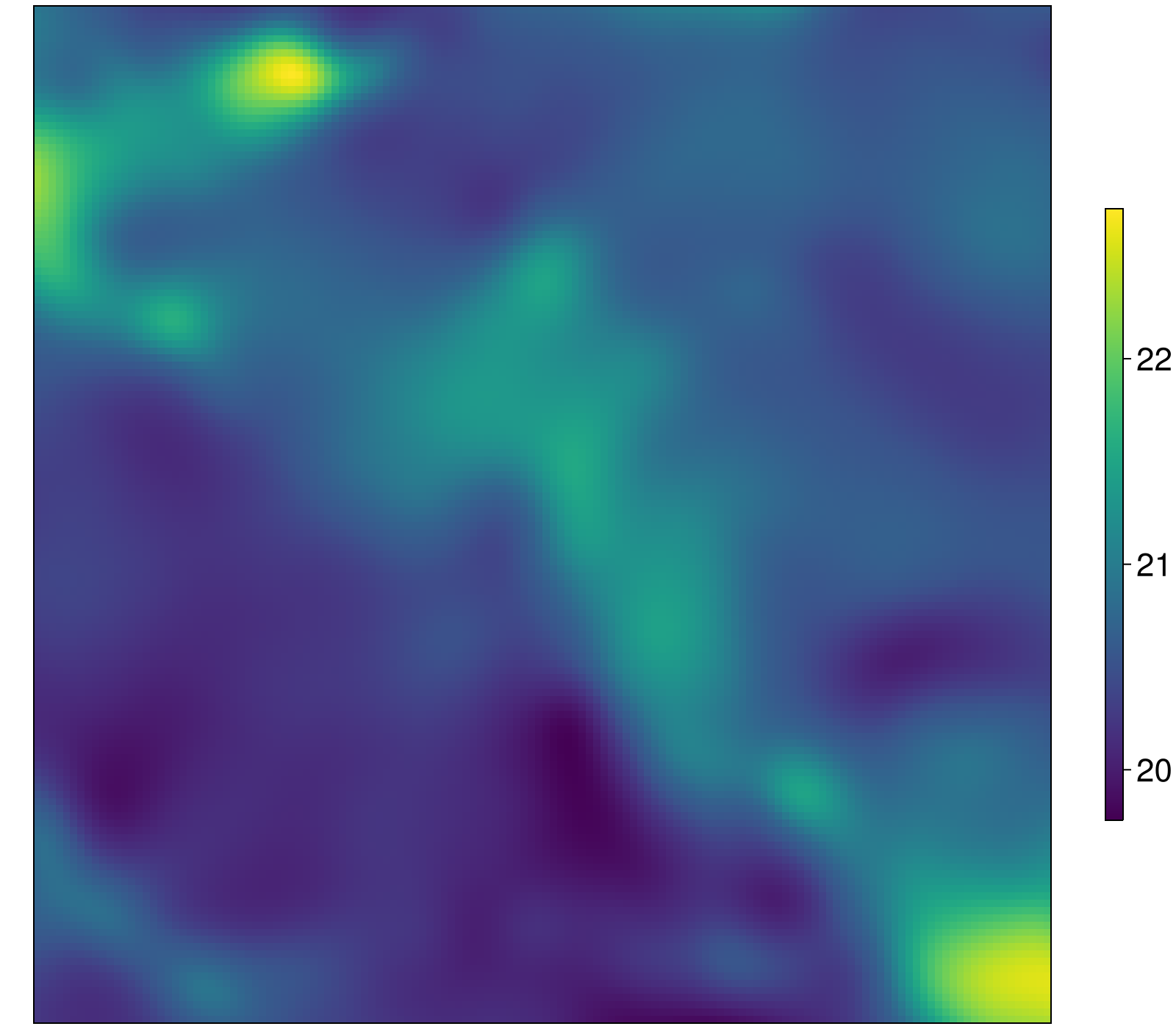
Example block output

The number of layers and the depth of viscous half-space are arbitrary parameters that have to be defined by the user. We here use a relatively shallow model (half-space begins at 300 km depth) with 1 equalisation layer and 3 intermediate layers:

mindepth = maximum(Tlitho) + 1e3
lb_vec = range(mindepth, stop = 300e3, length = 3)
lb = cat(Tlitho, [fill(lbval, Omega.Nx, Omega.Ny) for lbval in lb_vec]..., dims=3)

rlb = c.r_equator .- lb
nlb = size(rlb, 3)
lv_3D = 10 .^ cat([logeta_itp.(Lon, Lat, rlb[:, :, k]) for k in 1:nlb]..., dims=3);

To prevent extreme values of the viscosity, we require it to be larger than a minimal value, fixed to be $ 10^{16} \, \mathrm{Pa \, s} $. We subsequently generate a LayeredEarth that embeds all the information that has been loaded so far:

eta_lowerbound = 1e16
lv_3D[lv_3D .< eta_lowerbound] .= eta_lowerbound
p = LayeredEarth(Omega, layer_boundaries = lb, layer_viscosities = lv_3D)
niceheatmap(p.effective_viscosity)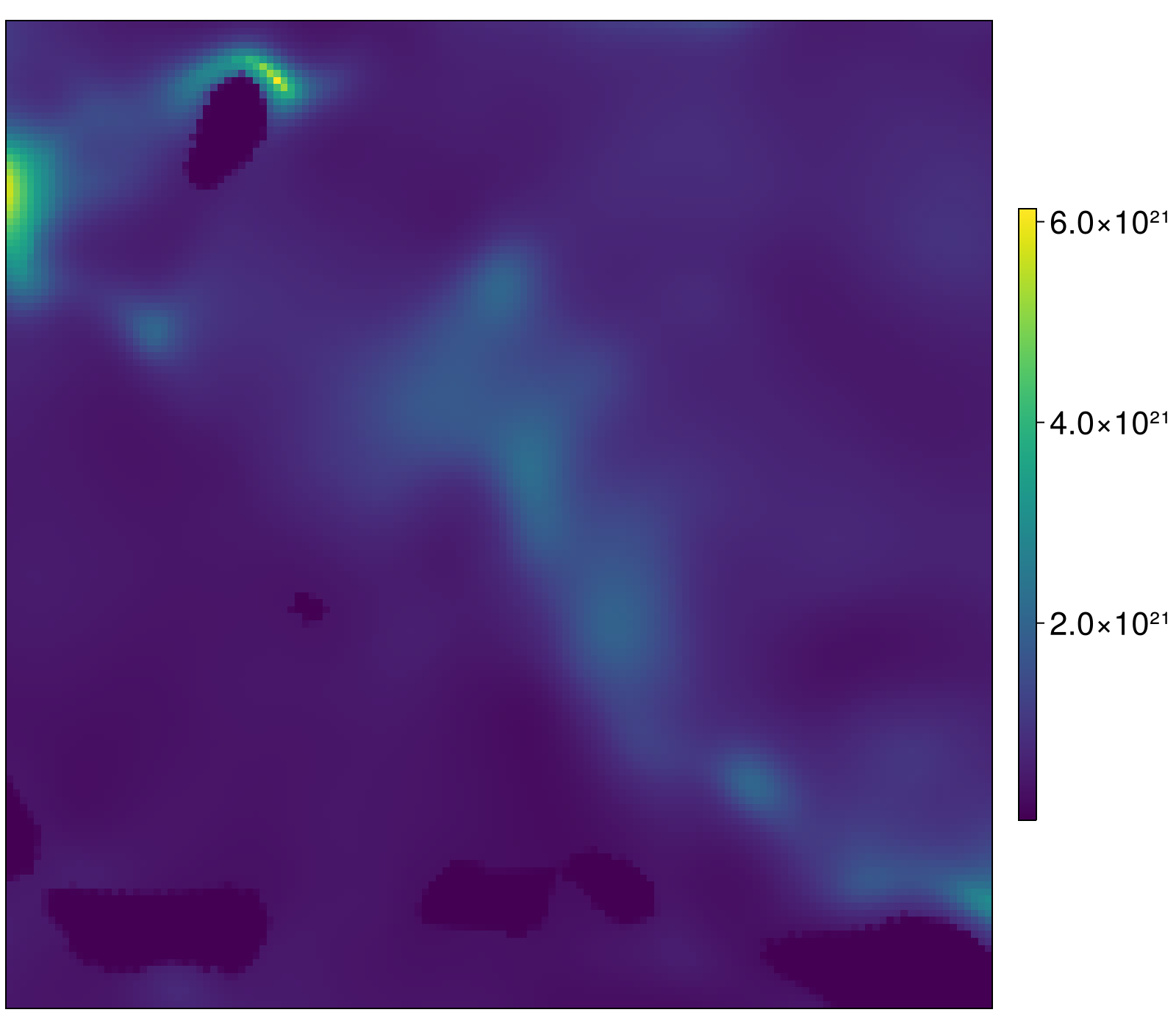
Example block output

We now load the ice thickness history from ICE6GD, again helped by the convenience of [`loaddataset`](@ref). We then create a vector of anomaly snapshots, between which FastIsostasy automatically interpolates linearly. To get an idea of ICE6G_D, the ice thickness anomaly is then visualised at LGM:

(lon, lat, t), Hice, Hitp = load_ice6gd()
dHice = [Hitp.(Lon, Lat, tk) - Hitp.(Lon, Lat, minimum(t)) for tk in t]
niceheatmap(Hitp.(Lon, Lat, -26) - Hitp.(Lon, Lat, 0))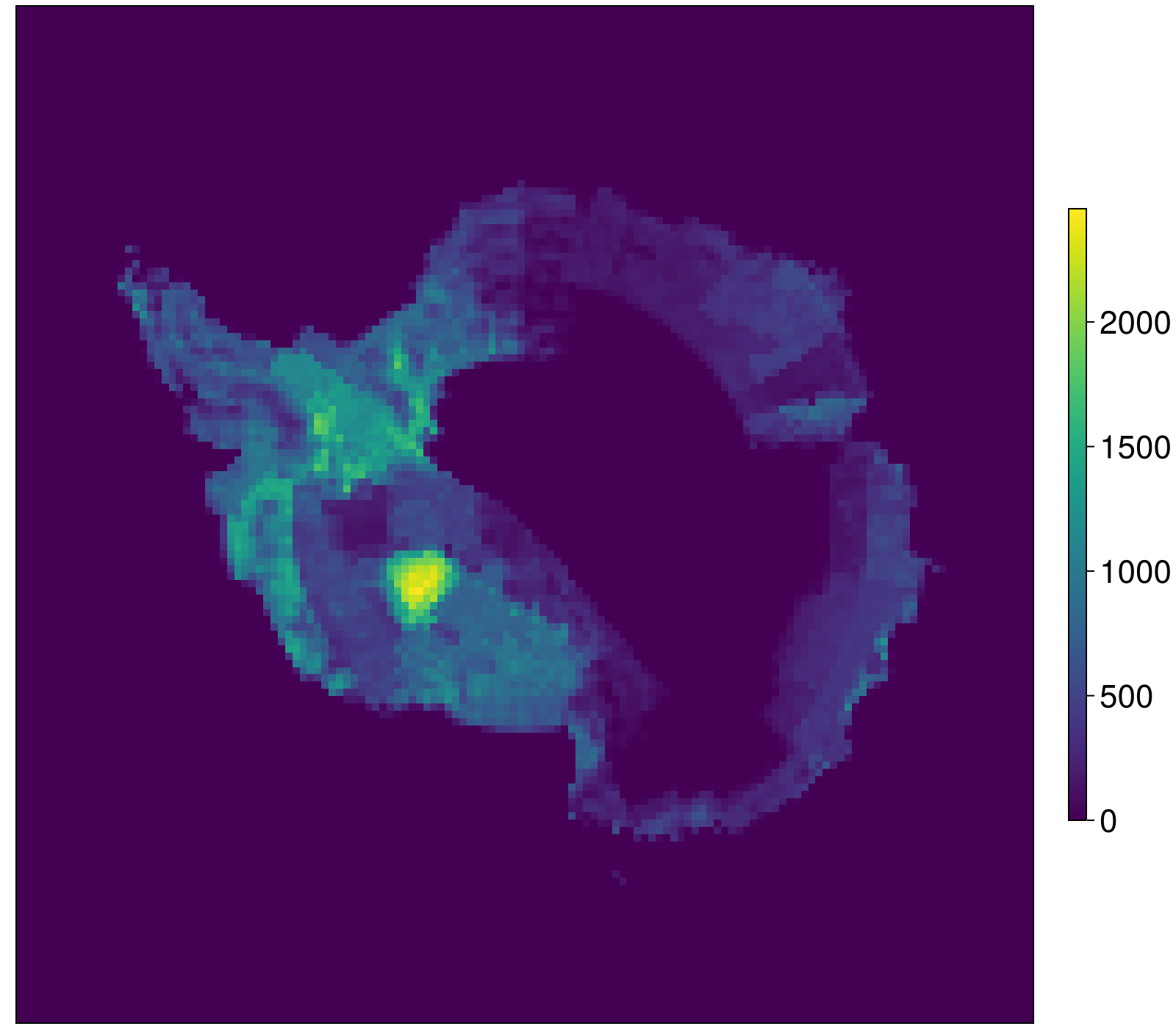
Example block output

Finally, defining and solving the resulting FastIsoProblem is done by running:

tsec = years2seconds.(t .* 1e3)
fip = FastIsoProblem(Omega, c, p, tsec, tsec, dHice)
solve!(fip)     # gives fip.out.computation_time = 53 s

The computation time of this last step is less than a minute on a modern i7 (Intel i7-10750H CPU @ 2.60GHz). and for a resolution of 50 km resolution! We visualise three snapshots of displacements that roughly correspond to LGM, the end of the meltwater pulse 1A and the present-day:

tplot = [-26, -12, 0]
fig = Figure(size = (1800, 600))
opts = ( colormap = :PuOr, colorrange = (-400, 400) )
for k in eachindex(tplot)
    ax = Axis(fig[1, k], aspect = DataAspect())
    hidedecorations!(ax)
    kfi = argmin( abs.(years2seconds(tplot[k] * 1e3) .- tsec) )
    heatmap!(ax, fip.out.u[kfi] + fip.out.ue[kfi]; opts...)
    println(kfi)
end
Colorbar(fig[1, 4], height = Relative(0.6); opts...)
fig
Example block output

The displayed fields are displacement anomalies w.r.t. to the last interglacial, defined as the reference for the ice thickness anomalies. In Swierczek-Jereczek et al., GMD, in rev., these computations are performed on a finer grid, with an interactive sea level, and show great agreement with a 3D GIA model that runs between 10,000-100,000 slower (however at with advantage of obtaining a global and richer output). You can find this more comprehensive example in the /publication_v1.0 folder of the GitHub repository.